本篇笔记主要写的是有关各类图算法的笔记。
图
定义
关于图（graph），有一系列的并不复杂的的定义，这里简单地做一些陈列。
图指的是由一系列顶点（vertex）以及连接它们的边（edge）的数据模型。
平行边指的是连接同一对顶点的一组边。
自环指的是顶点连接自己的一条边。
不含有平行边和自环的图被称为简单图（simple graph）。不做特殊说明时，我们说的图指的都是简单图。
两个顶点通过一条边相连接，则为相邻（neighbor）。
有向图指的是边 ab 和边 ba 不视作同一条边的图。无向图则是边 ab 和边 ba 视作同一条边的图。
无向图中，一个顶点的度数（degree）是指一端为它的边的数量。
有向图中，一个顶点的出度数指的是从它出发的边的数量，入度数则是到达它的边的数量。
路径（path）指的是一组顺序连接的边以及它们经过的顶点。简单路径是一条没有重复顶点的路径。
环（cycle，loop）是一条至少含有一条边且起点和终点相同的路径。简单环是一条除了起点终点必须相同、其余情况不含有重复顶点和边的环。
路径的长度指的是其中边的数量。
从一个顶点到任意一个顶点都存在至少一条路径的图叫做连通图（connected graph）。
非连通图是由若干个连通的子图构成的，它们被称为连通分量（connected components）。
树（tree）是一个无环连通图。
到这里就基本上足够讨论本篇中的内容了。
实现
从实现的角度来说，对于图而言其只需要维护边和顶点即可。它所需要维护的方法却可能比较复杂，例如我们需要有能够返回任意节点度数的函数、返回一个顶点邻居的函数、最大度数、判断顶点到另一个顶点是否存在路径的方法等。
基于不同的需求，图自然有很多不一样的数据结构表达方式。一个在性能和功能上均比较令人满意的方法是邻接表数组（adjacency array）。存储一个 vector<vector<int>> V，其中 V[i] 表示第 i 个顶点的邻居顶点的索引数组。为了方便下面的讨论，我们就采用这个方式来记录图。
无向图算法
DFS（深度优先搜索）
深度优先搜索（Depth First Search, DFS）是一种递归算法，可以形容为以下的步骤：
选择一个搜索起点，将它标记为已访问。
递归地访问它所有没有被标记过的邻居。
应用 DFS 的最经典的任务是查看给定图是否是连通图，这个问题等价于对于图 G 中的顶点 u，是否存在一条路径到达另一个顶点 v。这两个问题分别被称为连通性问题和单点路径问题，如上所述它们是等价的。
我们可以维护一个长度为顶点数量的 marked 数组，对于已经走过的数组进行一次标记。对于连通性问题， 借助 DFS 可以解决的几个子问题：
给定图是否是连通图：在 DFS 结束之后判断 marked 数组是否已经全部被标记，是则返回 true，否则返回 false。
给定图有几个连通分量：直到 marked 数组被全部标记前，维护 count，每次递归调用至底层时判断 marked 数组是否全部被标记。是则返回 count，否则 count++。
给定图中点 u 与点 v 是否处于同一个连通分量：从点 u 开始 DFS，如果 DFS 结束之后 marked 数组中 v 被标记为已访问，则说明处于同一个连通分量。
注意上面的第三个子问题其实和单点路径问题是完全一致的。
一个不具备任何功能的 DFS 如下所示：
在上面的这个实现中，我们只维护了 marked 数组，但并没有完成任何的任务。如果我们要解决子问题 1（给定图是否是连通图），则只需要在 DFS 结束的时候进行判断即可。
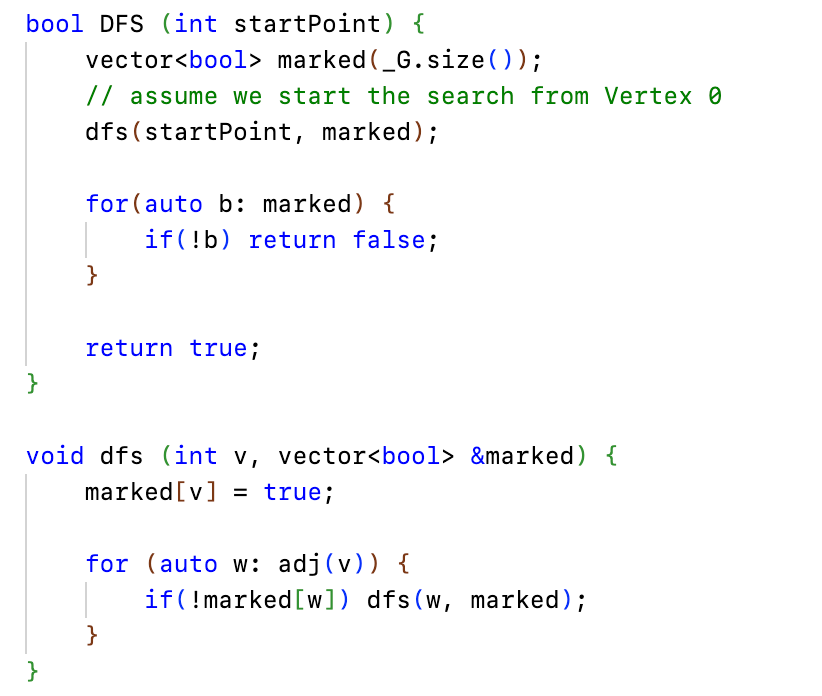
抽象的部分至此为止就差不多了。反应到现实问题中，我们要精准地在各个情景中识别出图、边、顶点的幻化。以下一些问题是 LeetCode 中 DFS 的一些可爱的展现形式。
BFS（广度优先搜索）
连通分量
最短路径算法
Dijkstra 算法
参考资料：
算法（第4版），Robert Sedgewick 著，中国工信出版集团/人民邮电出版社，谢路云译
Comments